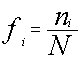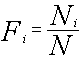NÚMEROS RACIONALES - SUMA DE FRACCIONES

PRACTICANDO  SUMA DE FRACCIONES

LINK : http://www.educaplus.org/play-93-Suma-de-fracciones.html





HACER  CLICK :    http://www.accedetic.es/fracciones/fracciones/index

NÚMEROS RACIONALES

Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por .

Representación de números racionales

Los números racionales se representan en la recta junto a los números enteros.

Los números racionales se representan en la recta junto a los números enteros.
1 Tomamos un segmento de longitud la unidad, por ejemplo.
2 Trazamos un segmento auxiliar desde el origen y lo dividimos en las partes que deseemos. En nuestro ejemplo, lo dividimos en 4 partes.
3 Unimos el último punto del segmento auxiliar con el extremo del otro segmento y trazamos segmentos paralelos en cada uno de los puntos, obtenidos en la partición del segmento auxiliar.

En la práctica se utilizan número racional y fracción como sinónimos.





PRACTICANDO :

http://www.vitutor.com/di/r/a_10e.html

• 
  

Los números racionales, son el conjunto de números fraccionarios y números enteros representados por medio de fracciones. Este conjunto está situado en la recta real numérica pero a diferencia de los números naturales que son consecutivos, por ejemplo :

a 4 le sigue 5 y a este a su vez le sigue el 6, y los números negativos cuya consecución se da así, a -9 le sigue -8 y a este a su vez le sigue -7; los números racionales no poseen consecución pues entre cada número racional existen infinitos números que solo podrían ser escritos durante toda la eternidad.
Todos los números fraccionarios son números racionales, y sirven para representar medidas. Pues a veces es más conveniente expresar un número de esta manera que convertirlo a decimal exacto o periódico, debido a la gran cantidad de decimales que se podrían obtener.

Definición de números racionales

Para decir, ¿Qué son números racionales? Podemos empezar por decir que, un número racional es una cifra o valor que puede ser referido como el cociente de dos números enteros o más precisamente, un número entero y un número natural positivo. Es decir que es un número racional, es un número que se escribe mediante una fracción.

Los números racionales son números fraccionarios, sin embargo los números enteros también pueden ser expresados como fracción, por lo tanto también pueden ser tomados como números racionales con el simple hecho de dar un cociente entre el número entero y el número 1 como denominador.

Al conjunto de los números racionales se lo denota con la letra ℚ, que viene de la palabra anglosajona “Quotient” traducción literal de cociente, y que sirve para recogerlos como subgrupo dentro de los números reales y junto a los números enteros cuya denotación es la letra Z. Por ello, en ocasiones se refieren a los números racionales como números ℚ.

Un número racional puede ser expresado de diferentes maneras, sin alterar su cantidad mediante fracciones equivalentes, por ejemplo ½ puede ser expresado como 2/4 o 4/8, debido a que estas son fracciones reducibles. Asimismo existe una clasificación de los números racionales dependiendo de su expresión decimal, estos son:
Los números racionales limitados, cuya representación decimal tiene un número determinado y fijo de cifras, por ejemplo 1/8 es igual a 0,125.

Los números racionales periódicos, de los cuales sus decimales tienen un número ilimitado de cifras, pero se diferencian de los números irracionales porque de esas cifras se puede descubrir un patrón definido mientras que en los números irracionales sus cifras decimales son infinitas y no-periódicas.
A su vez los números racionales periódicos se dividen en dos, los periódicos puros, cuyo patrón se encuentra inmediatamente después de la coma, por ejemplo 0,6363636363… y los periódicos mixtos, de los cuales el patrón se encuentra después de un número determinado de cifras, por ejemplo 5,48176363636363…

Propiedades de los números racionales

Existen para la suma y resta, y para la multiplicación y división, distintas propiedades de los números racionales, estos son:

Entre las propiedades de la suma y resta están:

Propiedad interna.- según la cual al sumar dos números racionales, el resultado siempre será otro número racional, aunque este resultado puede ser reducido a su mínima expresión si el caso lo
necesitara.

ab+cd=ef

Propiedad asociativa.- se dice que si se agrupa los diferentes sumandos racionales, el resultado no cambia y seguirá siendo un número racional. Veamos:

(ab+cd)−ef=ab+(cd−ef)

Propiedad conmutativa.- donde en la operación, si el orden de los sumando varía, el resultado no cambia, de esta manera:

ab+cd=cd+ab

Elemento neutro.- el elemento neutro, es una cifra nula la cual si es sumada a cualquier número racional, la respuesta será el mismo número racional.

ab+0=ab

Inverso aditivo o elemento opuesto.- es la propiedad de números racionales según la cual, existe un elemento negativo que anula la existencia del otro. Es decir que al sumarlos, se obtiene como resultado el cero.

ab−ab=0

Por otro lado, existen también las propiedades de los números racionales por parte de la multiplicación y la división, y estas son:
Propiedad interna.- en razón de que al multiplicar números racionales, el resultado también es un número racional.

ab×cd=ef

Esta además aplica con la división

ab÷cd=ef

Propiedad asociativa.- donde al agrupar diferentes factores la forma de la agrupación, no altera el producto.

(ab×cd)×ef=ab×(cd×ef)

Propiedad conmutativa.- aquí se aplica la famosa frase, el orden de los factores no altera el producto, entre los números racionales también funciona.

ab×cd=cd×ab

Propiedad distributiva.- al combinar sumas y multiplicaciones, el resultado es igual a la suma de los factores multiplicado por cada uno de los sumandos, veamos el ejemplo:

ab×(cd+ef)=ab×cd+ab×ef

Elemento neutro.- en la multiplicación y la división de números racionales, existe un elemento neutro que es el número uno, cuyo producto o cociente con otro número racional, dará como resultado el mismo número.

ab×1=ab 

 ab÷1=ab

Ejemplos de números racionales

Los números racionales son números fraccionarios, es decir que podríamos escribir cualquier cociente entre dos números enteros y llamarlo número racional, aquí un ejemplo

57

Aunque también podría ser expresado de esta manera:

5/7

Sin embargo, los números enteros también pueden ser incluidos dentro de los números Q, al formar un cociente con un número neutro, es decir de este modo:

3=31

Aunque también podríamos expresar el número entero 3, en forma de fracción, en el caso de necesitarlo en alguna operación matemática, pues al simplificarlo obtenemos la misma respuesta:

155=3

También encontramos números racionales enteros negativos, por ejemplo:

−6=−61

0,2424242424… también puede ser tomado como un número racional, pues sus decimales son periódicos, y podemos expresarlo en forma de fracción, así:

                              24/99

TABLAS Y DIAGRAMAS DE BARRAS

Diagrama de barras

El diagrama de barras (o gráfico de barras) es un gráfico que se utiliza para representar datos de variables cualitativas o discretas. Está formado por barras rectangulares cuya altura es proporcional a la frecuencia de cada uno de los valores de la variable.

Las principales características del diagrama de barras son:

• En el eje de abscisas se colocan las cualidades de la variable, si la variable es cualitativa, o los valores de dicha variable, si es discreta.
• En el eje de ordenadas se colocan las barras proporcionales a la frecuencia relativa o absoluta del dato.
• Las barras pueden ser horizontales o verticales, según si los valores de la variable se reflejan en el eje horizontal o vertical.
• Todas las barras deben tener el mismo ancho y no deben superponerse las unas con las otras.

Tipos de gráficos de barras

Existen cuatro tipos de gráficos de barras según las series de datos y como están estas representadas:

1. Gráfico de barras sencillo

Representa los datos de una única serie o conjunto de datos.

2. Gráfico de barras agrupado

• Representa los datos de dos o más series o conjuntos de datos.
• Cada serie se representa en un mismo color.
• Las barras se colocan una al lado de la otra por categoría de la variable para comparar las series de datos.

3. Gráfico de barras apilado

• Representa los datos de dos o más series o conjuntos de datos.
• Cada serie se representa en un mismo color.
• Cada barra representa una categoría de la variable, y se divide en segmentos que representan cada una de las series de datos.

4. Pirámide de población

Una pirámide de población es un diagrama de barras bidireccional que muestra la población por sexo y rangos de edad en un momento determinado.
En el eje vertical se representan los intervalos de edades. En el eje horizontal se representan los porcentajes de población. En una dirección se representarán los hombres y en el otro las mujeres.

Ejemplo

El jefe de una empresa pregunta a sus empleados cuando prefieren disfrutar de sus vacaciones. Les ofrece cinco quincenas.
Con las respuestas de los 290 trabajadores, construye una tabla:



Para visualizar mejor los datos, dibuja un diagrama de barras verticales.



Se puede observar como la inmensa mayoría de los trabajadores preferiría las vacaciones en las quincenas de agosto.

http://www.juntadeandalucia.es/averroes/~11001646/DATOS/BARRAS.htm

LINK  :OBSERVAR , PRACTICA   Y  RESUELVE  SECCIÓN  RECURSOS: 
  http://www.juntadeandalucia.es/averroes/~11001646/DATOS/INICIO.htm

:  PRACTICANDO :    LINK  http://www.edu.xunta.es/espazoAbalar/sites/espazoAbalar/files/datos/1285583725/contido/index.html

ESTADÍSTICA - POBLACIÓN Y MUESTRA

QUÉ ES LA ESTADÍSTICA?

HISTORIA

Establecer con absoluta claridad y precisión el proceso de desarrollo de esta ciencia que actualmente se llama Estadística, es una tarea difícil ya que la información que se dispone es fragmentada, parcial y aislada.
Es seguro que desde la antigüedad se realizaron inventarios de habitantes, bienes, productos, etc. Estos inventarios o censos (palabra derivada del latín cencere que significa valuar o tasar) se realizaron con fines catastrales, tributarios y militares.
En Egipto ya en el año 3050 a. c se tiene noticias de estadísticas destinadas a fines semejantes a los señalados y especialmente en la construcción de las pirámides.
En China en el año 2000 a. c. se conocen estudios similares. El nacimiento de Cristo coincide con la realización de un censo poblacional en gran escala en el Imperio Romano. Durante mucho tiempo se entendía por "estadística" la información relacionada con el gobierno, la palabra misma se deriva del latín statisticus o estatus que significa "del estado".
Ya en nuestra era, en el año 727, los árabes realizaron estadísticas similares en lo que hoy es España. En Inglaterra en el año 1083 y 1662 y el Alemania en 1741, se llevaron a cabo censos referentes a defunciones, nacimientos, enfermedades, posesión de bienes, migraciones y otros problemas y los datos obtenidos se utilizaron en la previsión y planificación. En América se realizaron encuestas mediante el sistema de "quipus".
El desarrollo científico de la estadística comienza recién en el siglo XVII, con la introducción en el pensum de estudio de las universidades en Alemania.
A comienzos del siglo XX, una nueva aportación de la escuela inglesa, preocupada por problemas de índole agropecuaria y biométrica coloca a la estadística en el tramo final de su establecimiento como ciencia.
En general las primeras aplicaciones de la estadística tuvieron que ver directamente con las actividades del estado. Se cree que la primera persona que hizo uso de la palabra estadística fue Godofredo Achenwall (1719-1772), profesor y economista alemán, escribió sobre el descubrimiento de una nueva ciencia que llamó estadística (palabra derivada de Staat que significa gobierno) y que definió como "el conocimiento profundo de la situación respectiva y comparativa de cada estado".

DEFINICIÓN

Existen muchas definiciones de Estadística, pero en síntesis la podemos definir como la ciencia rama de la Matemática que se ocupa de recolectar, organizar, presentar, analizar e interpretar información cuantitativa para obtener conclusiones válidas, solucionar problemas, predecir fenómenos y ayudar a una toma de decisiones más efectivas.

(Ver: Tipos de estadísticas)
Es muy frecuente enfrentarnos con fenómenos en los que es muy difícil predecir el resultado; así, no podemos dar una lista con las personas que van a morir con una cierta edad, o el sexo de un nuevo ser hasta que transcurra un determinado tiempo de embarazo.
Por tanto, el objetivo de la estadística es hallar las regularidades que se encuentran en los fenómenos de masa.

La palabra "estadística" suele utilizarse bajo dos significados distintos:

1º Como colección de datos numéricos.
Esto es el significado más vulgar de la palabra estadística. Se sobrentiende que dichos datos numéricos han de estar presentados de manera ordenada y sistemática. Una información numérica cualquiera puede no constituir una estadística, para merecer este apelativo, los datos han de constituir un conjunto coherente, establecido de forma sistemática y siguiendo un criterio de ordenación.
2º Como ciencia.
En este significado, la Estadística estudia el comportamiento de los fenómenos de masas. Como todas las ciencias, busca las características generales de un colectivo y prescinde de las particulares de cada elemento. Así por ejemplo al investigar el sexo de los nacimientos, iniciaremos el trabajo tomando un grupo numeroso de nacimientos y obtener después la proporción de varones.

APLICACIONES

La Estadística anteriormente sólo se aplicaba a los asuntos del Estado, pero en la actualidad la utilizan las compañías de seguros, empresarios, comerciantes, educadores, etc. No hay campo de la actividad humana que no requiera del auxilio de esta ciencia, así por ejemplo:
- El educador mediante la estadística podrá conocer si un estudiante lee muy bien o regular, si la asistencia es normal o irregular, si la estatura está en relación con la edad, media aritmética de rendimiento escolar en un período determinado, etc.
- El hombre de negocios realiza encuestas estadísticas para determinar la reacción de los consumidores frente a los actuales productos de la empresa y en el lanzamiento de los nuevos.
- El economista emplea una amplia gama de estadísticas para estudiar los planes de los consumidores y efectuar pronósticos sobre las tendencias de las actividades económicas
- El gerente de una empresa eléctrica proporciona un buen servicio a la comunidad mediante la variación estacional de las necesidades de carga
- El sociólogo trata de auscultar la opinión pública mediante encuestas, para determinar su preferencia por un candidato presidencial, o su posición frente a determinados problemas económicos, políticos o sociales
- El geólogo utiliza métodos estadísticos para determinar las edades de las rocas
- El Genetista determina las semejanzas entre los resultados observados y esperados en una experiencia genética se determina estadísticamente

FINES

- Conocer las características de un grupo de casos de estudio.
- Comparar entre los resultados actuales y los obtenidos en experiencias pasadas para determinar las causas que han influenciado en los cambios.
- Predecir lo que pude ocurrir en el futuro de un fenómeno.

OBJETIVOS

- Describir numéricamente las características de los conjuntos de observaciones. Esta etapa consiste en recopilar, organizar, tabular y presentar gráficamente los datos, proporcionando una visión cuantitativa de los fenómenos observados.
- Analizar los datos de manera objetiva con el fin de disponer de un concepto claro de universo o población y adoptar decisiones basadas en la información proporcionada por los datos de la muestra.
- Estimar o predecir lo que sucederá en el futuro con un fenómeno de una manera relativamente aceptable, así por ejemplo, podemos estimar cuál será la población del país dentro de un determinado número de años conociendo la actual.

MÉTODOS

- Recopilación.- Consiste en la obtención de datos relacionados con el problema motivo de estudio, utilizando instrumentos, tales como: cuestionarios, entrevistas, informes, memorias, etc.
- Organización.- Consiste en realizar una crítica, corrección, clasificación y tabulación de los datos obtenidos en el paso anterior.
Persentación.-- Consiste en mostrar datos de manera significativa y descriptiva. Los datos deben colocarse en un orden lógico que revele rápida y fácilmente el mensaje que contienen. La presentación se la puede hacer a través de gráficos estadísticos.
- Análisis.- Consiste en descomponer el fenómeno en partes y luego examinar cada una de ellas con el objetivo de lograr una explicación, haciendo uso, en su mayoría, de los cálculos matemáticos.
- Interpretación.- Consiste en un proceso mental, mediante el cual se encuentra un significado más amplio de los datos estadísticos con el objetivo de llegar a conclusiones para la toma de decisiones y solución de problemas.

CLASIFICACIÓN DE LA ESTADÍSTICA

Estadística Descriptiva o Deductiva

Es un proceso mediante el cual se recopila, organiza, presenta, analiza e interpreta datos de manera tal que describa fácil y rápidamente las características esenciales de dichos datos mediante el empleo de métodos gráficos, tabulares o numéricos, así por ejemplo:
Supóngase que un docente de Matemática calcula la calificación promedio de uno de sus cursos a su cargo. Como solo se está describiendo el desempeño del curso pero no hace ninguna generalización acerca de los diferentes cursos, en este caso el maestro está haciendo uso de la Estadística Descriptiva.
Estadística Inferencial o Inductiva
Llamada también inferencia estadística, la cual consiste en llegar a obtener conclusiones o generalizaciones que sobrepasan los límites de los conocimientos aportados por un conjunto de datos. Busca obtener información sobre la población basándose en el estudio de los datos de una muestra tomada a partir de ella, así por ejemplo:
Supóngase ahora que el docente de Matemática utiliza el promedio de calificaciones obtenidas por uno de sus cursos para estimar la calificación promedio de los 5 cursos a su cargo. Como se está realizando una generalización acerca los diferentes cursos, en este caso el maestro usa la Estadística Inferencial.

CONCEPTOS Y DEFINICIONES BÁSICAS

POBLACIÓN

Llamado también universo o colectivo es el conjunto de todos los elementos que tienen una característica común.
Una población puede ser finita o infinita. Es población finita cuando está delimitada y conocemos el número que la integran, así por ejemplo: Estudiantes de la Universidad UTN. Es población infinita cuando a pesar de estar delimitada en el espacio, no se conoce el número de elementos que la integran, así por ejemplo: Todos los profesionales universitarios que están ejerciendo su carrera.

MUESTRA

Es un subconjunto de la población. Ejemplo: Estudiantes de 2do Semestre de la Universidad UTN. Sus principales características son:

Representativa.- Se refiere a que todos y cada uno de los elementos de la población tengan la misma oportunidad de ser tomados en cuenta para formar dicha muestra.

Adecuada y válida.- Se refiere a que la muestra debe ser obtenida de tal manera que permita establecer un mínimo de error posible respecto de la población.

Para que una muestra sea fiable, es necesario que su tamaño sea obtenido mediante procesosmatemáticos que eliminen la incidencia del error.

Para calcular el tamaño de la muestra suele utilizarse la siguiente fórmula:

Donde:

n = el tamaño de la muestra. N = tamaño de la población.

Desviación estándar de la población que, generalmente cuando no se tiene su valor, suele utilizarse un valor constante de 0,5.

Z = Valor obtenido mediante niveles de confianza. Es un valor constante que, si no se tiene su valor, se lo toma en relación al 95% de confianza equivale a 1,96 (como más usual) o en relación al 99% de confianza equivale 2,58, valor que queda a criterio del encuestador.

e = Límite aceptable de error muestral que, generalmente cuando no se tiene su valor, suele utilizarse un valor que varía entre el 1% (0,01) y 9% (0,09), valor que queda a criterio del encuestador.

Ejemplo ilustrativo: Calcular el tamaño de la muestra de una población de 1000 elementos.
Solución:

Se tiene N=1000, y como no se tiene los demás valores se tomará o=0,5 , Z = 1,96 y e = 0,05. Reemplazando valores en la fórmula se obtiene:

ELEMENTO O INDIVIDUO

Unidad mínima que compone una población. El elemento puede ser una entidad simple (una persona) o una entidad compleja (una familia), y se denomina unidad investigativa.

DATOS ESTADÍSTICOS

Son medidas, valores o características susceptibles de ser observados y contados. Como por ejemplo, la edad de los estudiantes de la Universidad UTN.

Los datos estadísticos pueden ser clasificados en cualitativos (la diferencia entre ellos es de clase y no de cantidad), cuantitativos (representan magnitudes), cronológicos (difieren en instantes o períodos de tiempo) y geográficos (referidos a una localidad).
Los datos estadísticos se obtienen de fuentes primarias (obtenidos directamente sin intermediarios valiéndose de observaciones, encuestas, entrevistas y sondeos de opinión) y fuentes secundarias (obtenidos a través de intermediarios valiéndose de textos, revistas, documentos, publicaciones de prensa, y demás trabajos hechos por personas o entidades).

CENSO

Es una técnica de recolección de datos estadísticos que se realiza a toda la población

ENCUESTA

Es la técnica que nos permite recolectar datos estadísticos que se realiza una muestra de la población.
Se clasifica en:
- Descriptiva.- Cuando registra datos referentes a las características de los elementos o individuos.
- Explicativa.- Cuando averigua las causas o razones que originan los fenómenos.
- Mixtas.- Cuando es descriptiva y explicativa.
- Por muestreo.- Cuando recolecta información de grupos representativos de la población.
Su estructura es:
- Nombre de la institución que auspicia la encuesta.
- Tema de la encuesta.
- Objetivos de la encuesta.

- Datos informativos: Lugar, fecha, y otros datos que se considere necesario según la naturaleza de la información estadística a encuestarse.

- Instrucciones para el encuestado para que sepa la forma de llenar la encuesta.
- Cuestionario o listado de preguntas (cerradas, abiertas, o ambas a la vez) sobre los diferentes aspectos motivo de estudio.
- Frase de agradecimiento al encuestado, como por ejemplo, ¡Gracias por su colaboración!
Las diferentes tipos de preguntas pueden ser:
- Abiertas.- Son aquellas en la cual el encuestado construye la respuesta de manera libre según su opinión y de la manera que él desea. Ejemplo: ¿Qué piensa usted sobre la política educativa del actual gobierno?
- Cerradas o dicotómicas.- Sólo pueden ser contestadas por un "sí" o por un "no". Ejemplo: ¿Está
usted de acuerdo con la política educativa del actual gobierno?

Si ( ) No ( )

Como es obvio, la respuesta será forzosamente una de las alternativas planteadas: Las preguntas cerradas son fáciles de tabular y facilitan la cuantificación mediante la asignación de puntuaciones.
- Preguntas de elección múltiple o categorizada: Se trata en cierto modo de preguntas cerradas que, dentro de los extremos de una escala permiten una serie de alternativas de respuestas cuyos matices son fijados de antemano. Presentan dos formas: En abanico y de estimación
- Preguntas con respuesta en abanico: Estas preguntas permiten contestar señalando una o varias respuestas presentadas junto con la pregunta. Por ejemplo: Indique otras alternativas que considere importantes para mejorar la educación en nuestro país.
- Preguntas de Estimación: Son preguntas cuantitativas que introducen diversos grados de intensidad creciente o decreciente para un mismo ítem. Ejemplos:
-¿Cómo calificaría la política educativa del gobierno actual?
Excelente ( ) Muy Buena ( ) Regular ( ) Deficiente ( )
-¿En qué porcentaje está de acuerdo con la política educativa del gobierno actual?
100% ( ) 75% ( ) 50% ( ) 25% ( ) 0% ( )
- ¿Le interesa conocer el modelo educativo vigente?
Nada ( ) Poco ( ) Algo ( ) Mucho ( )
¿Piensa culminar sus estudios superiores?
Sí ( ) Probablemente Sí ( ) No ( ) Aún no decido ( )

VARIABLE

Son caracteres susceptibles a cambio y pueden tener diferentes valores en cada elemento o individuo.
Clasificación
- Variable Cualitativa
Son atributos que se expresan mediante palabras no numéricas. Como por ejemplo, profesión,religión, marca de automóvil, estado civil, sexo, raza, etc.
- Variable Cuantitativa
Es toda magnitud representada por números. Como por ejemplo, peso, estatura, número de habitantes, etc.
- Variable Discreta
Es una característica cuantitativa representada por números enteros o exactos, que generalmente resultan del proceso de conteo, como por ejemplo: número de estudiantes de la promoción del año anterior.
- Variable Continua
Es una característica cuantitativa que puede tomar cualquier valor representado por un número racional, que generalmente resultan del proceso de medición, como por ejemplo, tiempo destinado a estudiar Estadística
Niveles de medición
- Nivel Nominal
Cuando los datos sólo pueden contarse y clasificados en categorías, no existe un orden específico entre las clases. Como por ejemplo, se cuentan cuántos hombres y cuántas mujeres asisten a determinado evento.
- Nivel Ordinal
Cuando se ordenan los datos por jerarquías, una categoría es mayor que otra. Como por ejemplo, excelente es mejor que bueno o bueno es mejor que regular. Otro ejemplo: Una persona puede tener mucho o poco dinero.
- Nivel de Intervalos
Cuando se incluye todas las características del nivel ordinal, pero la diferencia entre los valores tiene un significado medido en unidades iguales que son comunes y constantes, que permiten asignar números reales a todos los miembros de la clase ordenada, facilitando el establecimiento de diferencias en grados de propiedad y entre objetos sobre la base de una medida. Como por ejemplo: La diferencia entre 70 kilogramos y 60 kilogramos, es de 10 kilogramos. Otro ejemplo: Si la temperatura de hoy es de 20 grados centígrados y la de ayer fue de 25 grados centígrados, se sabe que la de hoy es 5 grados centígrados más baja que la de ayer.
- Nivel de Razón o Cociente
Este es el nivel de medición "más alto", tiene todas las características del nivel de intervalos y además en este nivel de medición el cero tiene significado (así si se tiene 0 dólares, entonces no se poseen fondos), y la razón (o cociente) entre dos números también es significativa (Un estudiante obtiene una calificación de 3/10 y otro 6/10, el segundo estudiante obtiene el doble que el primero).


Variables y atributos.
Como hemos visto, los caracteres de un elemento pueden ser de muy diversos tipos, por lo que los podemos clasificar en: dos grandes clases:
Variables Cuantitativas.
Variables Cualitativas o Atributos.
Las variables cuantitativas son las que se describen por medio de números, como por ejemplo el peso, altura, edad, número de suspendidos…
A su vez este tipo de variables se puede dividir en dos subclases:

• Cuantitativas discretas. Aquellas a las que se les puede asociar un número entero, es decir, aquellas que por su naturaleza no admiten un fraccionamiento de la unidad, por ejemplo número de hermanos, páginas de un libro, etc.
• Cuantitativas continuas: Aquellas que no se pueden expresar mediante un número entero, es decir, aquellas que por su naturaleza admiten que entre dos valores cualesquiera la variable pueda tomar cualquier valor intermedio, por ejemplo peso, tiempo. etc.

No obstante en muchos casos el tratamiento estadístico hace que a variables discretas las trabajemos como si fuesen continuas y viceversa.
Los atributos son aquellos caracteres que para su definición precisan de palabras, es decir, no le podemos asignar un número. Por ejemplo sexo, profesión, estado civil, etc.
A su vez las podemos clasificar en:

• Ordenables: Aquellas que sugieren una ordenación, por ejemplo la graduación militar, el nivel de estudios, etc.
• No ordenables: Aquellas que sólo admiten una mera ordenación alfabética, pero no establece orden por su naturaleza, por ejemplo el color de pelo, sexo, estado civil, etc.

FRECUENCIAS

- Frecuencia Absoluta ( )
Es el número de veces que se repite el valor de cada variable. La suma de frecuencias absolutas es siempre al total de datos observados.
- Frecuencia Relativa ( )
Indica la proporción con que se repite un valor. Es el cociente entre la frecuencia absoluta y el número total de datos. La suma de las frecuencias relativas es siempre 1

- Frecuencia Acumulada ( )

Indica el número de valores que son menores o iguales que el valor dado. Es la suma de la frecuencia absoluta primera con la segunda, este valor con la tercera, y así sucesivamente.

- Frecuencia Porcentual ( )

Llamada también frecuencia relativa porcentual. Se obtiene multiplicando la frecuencia relativa por 100. La suma de las frecuencias porcentuales es siempre 100%. Se calcula así:

- Frecuencia Relativa Acumulada ( )

Es la suma de la frecuencia relativa primera con la segunda, este valor con la tercera, y así sucesivamente.

- Frecuencia Relativa Acumulada Porcentual ( )

Indica el número de valores que son menores o iguales que el valor dado. Se obtiene multiplicando la frecuencia relativa acumulada por 100. Se calcula así:

Ejemplo ilustrativo:

Calcular las diferentes frecuencias de las siguientes calificaciones evaluadas sobre 10 obtenidas de 40  estudiantes en la asignatura de Estadística sin agrupar en clases:

Leer más: http://www.monografias.com/trabajos96/conceptos-basicos-estadistica-descriptiva-e-inferencial/conceptos-basicos-estadistica-descriptiva-e-inferencial.shtml#ixzz3WM9CwBML

Distintos Tipos de Frecuencia:
Una de los primeros pasos que se realizan en cualquier estudio estadístico es la tabulación de resultados, es decir, recoger la información de la muestra resumida en una tabla en la que a cada valor de la variable se le asocian determinados números que representan el número de veces que ha aparecido, su proporción con respecto a otros valores de la variable, etc. Estos números se denominan frecuencias: Así tenemos los siguientes tipos de frecuencia:
Frecuencia absoluta:
La frecuencia absoluta de una variable estadística es el número de veces que aparece en la muestra dicho valor de la variable, la representaremos por n_i
Frecuencia relativa:
La frecuencia absoluta, es una medida que está influida por el tamaño de la muestra, al aumentar el tamaño de la muestra aumentará también el tamaño de la frecuencia absoluta. Esto hace que no sea una medida útil para poder comparar. Para esto es necesario introducir el concepto de frecuencia relativa, que es el cociente entre la frecuencia absoluta y el tamaño de la muestra. La denotaremos por f_i

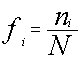
Donde N = Tamaño de la muestra
Ver: PSU: Estadística; Pregunta 05_2006
Frecuencia Absoluta Acumulada:
Para poder calcular este tipo de frecuencias hay que tener en cuenta que la variable estadística ha de ser cuantitativa o cualitativa ordenable. En otro caso no tiene mucho sentido el cálculo de esta frecuencia. La frecuencia absoluta acumulada de un valor de la variable, es el número de veces que ha aparecido en la muestra un valor menor o igual que el de la variable y lo representaremos por N_i.
Frecuencia Relativa Acumulada:
Al igual que en el caso anterior la frecuencia relativa acumulada es la frecuencia absoluta acumulada dividido por el tamaño de la muestra, y la denotaremos por F_i

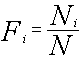Porcentaje Acumulado:
Análogamente se define el Porcentaje Acumulado y lo vamos a denotar por P_i como la frecuencia relativa acumulada multiplicada por 100.

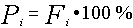Ejemplo:
Cuando se manejan conjuntos extensos de datos, el procedimiento preliminar más adecuado consiste en distribuirlos en clases o categorías de acuerdo con el número de casos que pertenecen a cada una de dichas clases.
 Por ejemplo, se quiere estudiar el puntaje que alcanzan los alumnos universitarios en la asignatura de    Educación Física. La escala de notas va del 0% al 100%, obteniéndose la siguiente colección de valores:
                          75-   82   -  68  -  90  -   62  -   88  -   88   -   73
                          60-   93   -  71  -   59  -    75  -   87   -   74   -  62
                          95-   78   -  82  -   75   -   94  -   77   -   69   -  74
                          89-   83   -  75   -  95   -   60  -  79   -   97   -  97
                          78-   85   -  76   -  65   -   73  -   67   -   88   -  78
                          62-   76   -  73   -  81   -   72  -    63  -   76   -  75
Para facilitar el análisis de los datos, éstos se ordenan en forma creciente, es decir, de menor a mayor (también puede ordenarse en forma decreciente).
El modo más sencillo de agrupar los datos, es mediante una tabla de datos, que indique, para cada uno de los valores de la colección, el número de veces que aparece, es decir, su frecuencia de aparición.
Distribuciones de frecuencia
Frecuencia absoluta (n_i): corresponde al número de veces que se observa dicho valor, o en otras palabras al número de veces que se presenta un cierto dato.
       Para agrupar los datos por su frecuencia, se deben seguir los siguientes pasos:
       1) Se ordenan los datos en orden creciente o decreciente.   
       2) Se cuenta la frecuencia absoluta de cada valor (cuántas veces se repite cada magnitud)
   De acuerdo a los datos anteriores, se observa que el número menor es 59 y el número mayor es 97.

Puntaje	Frecuencia absoluta (ni)
59	1
60	2
61	0
62	3
63	1
64	0
65	1
66	0
67	1
68	1
69	1
70	0
71	1
72	1
73	3
74	2
75	5
76	3
77	1
78	3
79	1
80	0
81	1
82	2
83	1
84	0
85	1
86	0
87	1
88	3
89	1
90	1
91	0
92	0
93	1
94	1
95	2
96	0
97	2
Frecuencia total	(N) 48

La Tabla de distribución de frecuencias hecha anteriormente sirve para facilitar el estudio de los valores estadísticos. El puntaje corresponde a la variable estadística (primera columna) y las veces que se repite la variable (segunda columna), a la frecuencia absoluta.
Frecuencia total (F): corresponde  la suma de las frecuencias absolutas de cada uno de los valores de la variable.
Una vez que se ha construido la Tabla de distribución de frecuencias, ésta debe ampliarse con otras tres columnas más, que corresponderán a la frecuencia absoluta acumulada, frecuencia relativa y frecuencia porcentual.
Frecuencia absoluta Acumulada (N_i ): es la suma de las frecuencias absolutas de cada intervalo. La frecuencia acumulada hasta el último intervalo es igual a la frecuencia total de toda la distribución.
Si se amplía la Tabla de distribución del ejemplo, la frecuencia absoluta acumulada se obtiene sumando el número que está escrito en una línea con el número de la línea siguiente.

Puntaje	Frecuencia absoluta (ni )	Frecuencia absoluta acumulada (Ni)
59	1	1
60	2	3
61	0	3
62	3	6
63	1	7
64	0	7
65	1	8
66	0	8
67	1	9
68	1	10
69	1	11
70	0	11
71	1	12
72	1	13
73	3	16
74	2	18
75	5	23
76	3	26
77	1	27
78	3	30
79	1	31
80	0	31
81	1	32
82	2	34
83	1	35
84	0	35
85	1	36
86	0	36
87	1	37
88	3	40
89	1	41
90	1	42
91	0	42
92	0	42
93	1	43
94	1	44
95	2	46
96	0	46
97	2	48
Frecuencia total	(N) 48

La frecuencia absoluta acumulada sirve para responder, por ejemplo, la siguiente pregunta: ¿Cuántos alumnos obtuvieron nota inferior a 80?; la respuesta es 31 alumnos.   

Frecuencia relativa (f_i): >corresponde a la razón (división) entre la frecuencia absoluta (n_i) y el número total (N) de individuos de la población.

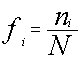
Puntaje	Frecuencia absoluta (ni )	Frecuencia absoluta acumulada (Ni)	Frecuencia relativa (fi )
59	1	1	0,02083 (1 : 48)
60	2	3	0,0416  (2  : 48)
61	0	3	0
62	3	6	0,0625
63	1	7	0,02083
64	0	7	0
65	1	8	0,02083
66	0	8	0
67	1	9	0,02083
68	1	10	0,02083
69	1	11	0,02083
70	0	11	0
71	1	12	0,02083
72	1	13	0,02083
73	3	16	0,0625
74	2	18	0,0416
75	5	23	0,10416
76	3	26	0,0625
77	1	27	0,02083
78	3	30	0,0625
79	1	31	0,02083
80	0	31	0
81	1	32	0,02083
82	2	34	0,0416
83	1	35	0,02083
84	0	35	0
85	1	36	0,02083
86	0	36	0
87	1	37	0,02083
88	3	40	0,0625
89	1	41	0,02083
90	1	42	0,02083
91	0	42	0
92	0	42	0
93	1	43	0,02083
94	1	44	0,02083
95	2	46	0, 0416
96	0	46	0
97	2	48	0,0416
Frecuencia total	(N) 48		1

La suma de las frecuencias relativas es 1
Frecuencia relativa porcentual: es la frecuencia relativa expresada en porcentajes (%)

Pi	=	f i	●	100
		N

Puntaje	(ni )	(Ni)	(fi )	% (Pi %)
59	1	1	0,02083 (1 : 48)	2,083
60	2	3	0,0416  (2  : 48)	4,16
61	0	3	0	0
62	3	6	0,0625	6,25
63	1	7	0,02083	2,083
64	0	7	0	0
65	1	8	0,02083	2,083
66	0	8	0	0
67	1	9	0,02083	2,083
68	1	10	0,02083	2,083
69	1	11	0,02083	2,083
70	0	11	0	0
71	1	12	0,02083	2,083
72	1	13	0,02083	2,083
73	3	16	0,0625	6,25
74	2	18	0,0416	4,16
75	5	23	0,10416	10,416
76	3	26	0,0625	6,25
77	1	27	0,02083	2,083
78	3	30	0,0625	6,25
79	1	31	0,02083	2,083
80	0	31	0	0
81	1	32	0,02083	2,083
82	2	34	0,0416	4,16
83	1	35	0,02083	2,083
84	0	35	0	0
85	1	36	0,02083	2,083
86	0	36	0	0
87	1	37	0,02083	2,083
88	3	40	0,0625	6,25
89	1	41	0,02083	2,083
90	1	42	0,02083	2,083
91	0	42	0	0
92	0	42	0	0
93	1	43	0,02083	2,083
94	1	44	0,02083	2,083
95	2	46	0, 0416	4,16
96	0	46	0	0
97	2	48	0,0416	4,16
Frecuencia total	(N)48		1	100  %

En el ejemplo el rango de los datos es:

                                                   Rango: 97 -  59  =  38

Rango: Corresponde a la diferencia (resta) entre el mayor y el menor de los datos
Ver  Medidas estadísticas
Fuente Internet:
http://thales.cica.es/rd/Recursos/rd97/UnidadesDidacticas/53-1-u-punt14.html